
An Introduction to Telescopes
by Ronen Sarig
As I set about the goal of documenting the telescopes that I designed in recent years, I realized that I had a major problem: the specifics fall under an incredibly esoteric field. I could write a report that would intrigue my colleagues in the optics industry - but my audience would be vastly limited. Therefore, in order to broaden the impact of the report, I decided to write a mini-lecture on optics - specifically pertaining to telescopes. The goal is that by the end of this guide, someone without previous optics knowledge will be able to understand my reports on telescope design!
The reader might note that this guide is nearly devoid of formulas. This is intentional - I believe that knowledge is best gained by understanding concepts. I find that complex formulas tend to confuse and intimidate beginners (although perhaps I’m merely projecting my own experiences.)
A final disclaimer: for many of the concepts described below, I will make simplifications or generalizations that may offend those of you who have studied optics. I apologize in advance: while many of these topics deserve an entire devoted book, that level of detail would serve to distract from my points.
Imaging Systems
We will begin our discussion about telescopes by introducing the concept of an imaging system. Most people have used imaging systems - generally in the form of a digital camera.
The purpose of an imaging system is to capture light emitted from an object on a sensor - a device capable of measuring light intensity over an area. We will explore two types of sensors:
First, we will focus on the former sensor type. The human eye is more complex than even the most sophisticated digital camera sensors, so it will be addressed later.
An electronic sensor generally takes the following form: the sensor has a flat, rectangular face, which is divided into a grid. Each square in the grid is called a pixel. The sensor is able to detect when light strikes a given pixel, and can communicate this information to a computer. Later, the data can be displayed, creating a photograph.

An image sensor on a flexible circuit board
By C-M - Own work, CC BY-SA 3.0, source
Consider the following scenario: we want to record an image of a flat wall. The wall displays a grid pattern, which we will attempt to map onto the pixels of the sensor. So, we aim our sensor at the wall:

Sensor facing the wall
To simplify the discussion, at times we may view the scene from the side, in two dimensions. The reader can assume that any concepts introduced in this orientation apply to the other dimension as well:

Side view of sensor facing the wall
We will assume that the wall is a diffuse emitter: this means that each point on the wall is giving off light in all directions. As is shown below, light from every square on the wall reaches every pixel on the sensor.
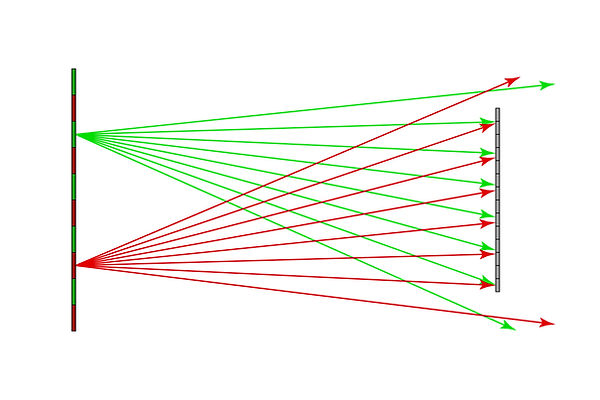
All pixels will receive rays from both red and green wall tiles
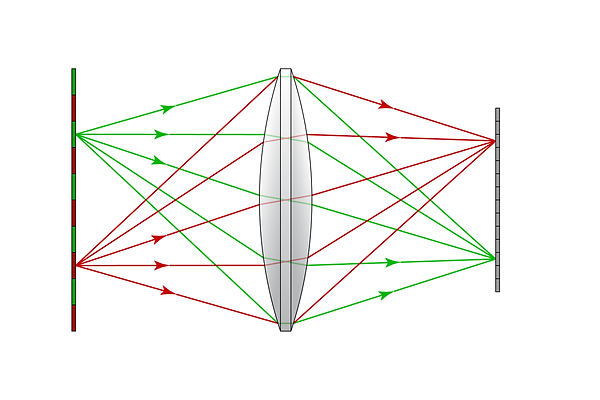
If this data were displayed, it would appear as an unintelligible blur. Those of you who have tried taking a photo through a detachable-lens camera without a lens have witnessed this effect. This is where lenses come into play: we have devised objects that, when placed in the light path, will force all light emanating from each point on the source to convene at a corresponding pixel on the sensor; These objects are called lenses.

A lens is placed between the object and the sensor
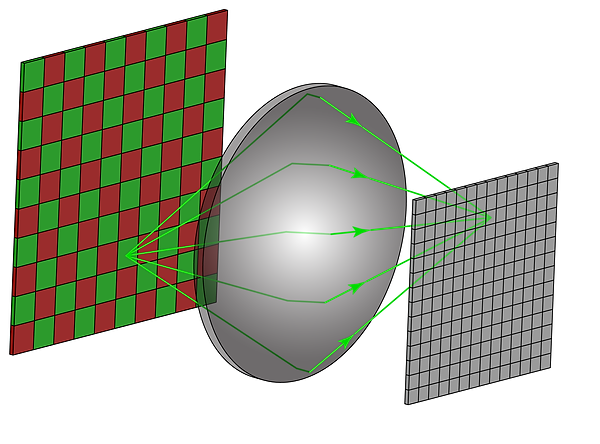
The lens focuses light from a single point on the wall to a single pixel on the sensor
The lens flips the image as it focuses light: on the target, the green square is above the red square. On the sensor, the orientation is reversed. This flipping effect occurs on both the horizontal and vertical axis.
Using a lens, we can construct a 1:1 mapping from points on an object to pixels on a sensor. By displaying the data collected by the sensor on an electronic screen or a print - we’ve effectively created a photograph of the object.
In this brief introduction, I have described what lenses do - but not why they work. The latter can be explained using a field called quantum electrodynamics. However, to explore that topic here would be a major digression. Furthermore, I don’t consider myself qualified to speak on that subject, as my own understanding is tenuous at best. Instead, I will point interested readers to Richard Feynman’s QED: The Strange Theory of Light and Matter, and Fermat’s Principle.
Telescopes: a Specific Type of Imaging System
A telescope is a type of imaging system. It has at least one powered (curved) optical element, and a sensor. In the previous example, the optical element was a single lens. The rest of the telescope is simply a structure meant to hold the optical elements and sensor in position. However, in order to observe the heavens, we must make some changes to our imaging system.
Previously, the lens was placed halfway between the target and the sensor. If we were to image the Orion Nebula with such a setup, the lens would be placed approximately 672 light years from earth; This is impractical with today’s technology. (Voyager 1 is currently the farthest human-made object from the earth, at 22.2 billion km - or 0.002 LY.)
Luckily, by adjusting the shape of the lens, we are able to change the distances between the object, lens, and sensor. The distance from the lens to the sensor is set to something reasonable: on the order of cm, rather than LY. Next, the distance from lens to target must be decided.
Telescopes are designed specifically for imaging objects at very large distances. The distances are so large, in fact, that we can consider them to be infinite. Geometrically, this is equivalent to treating all rays entering the telescope from a given point as parallel to each other.
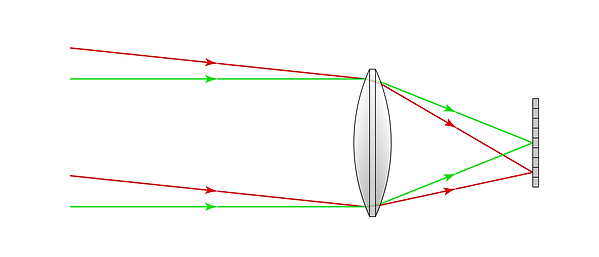
Each set of parallel rays entering the system converges to a unique pixel
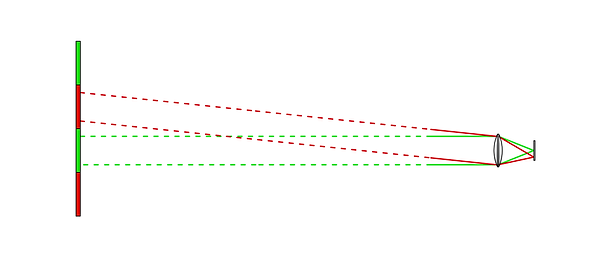
Rays from large, distant objects can be approximated as parallel
Let us validate the math behind this simplification:
-
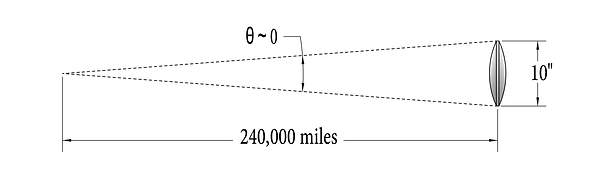
Assume a telescope diameter of 10”, and we are imaging the moon (the closest celestial body to earth, at 240,000 miles)
-
The largest angle between rays emitted from a point on the moon (as seen by our telescope) can be calculated as arcsine (10” / 240,000 miles) = 3.8E-8°. For parallel rays, this number would be 0. (See diagram below)
-
Treating these rays as parallel does not introduce enough error to be perceived by a camera sensor.
-
This error is further reduced for farther objects, because the largest angle between light rays is even smaller.
-
This scenario conveniently avoids another issue that complicates other types of imaging systems: depth of field.
_pn.png)
If the distance to the target is much larger than the diameter of the lens, the parallel ray approximation is valid.
The focal length of a lens is defined as the distance from the lens at which parallel light rays converge:

A lens with 1 m focal length focuses parallel light rays at 1 m
Focal Length and Aperture
Two key parameters are used in specifying the basic properties of a telescope: focal length and aperture. Camera lenses are specified in the same way. We will define aperture first, because it is the simpler of the two; Put plainly, aperture is the diameter of the optical system. The larger the aperture, the more light can be collected in a given period of time. Given that many celestial bodies are too dim to be seen by the naked eye, light collection is a critical parameter in telescope design.
Aperture size is one of three factors that determines how bright an image appears. The other two factors depend on the sensor itself: exposure time, and sensitivity. Exposure time varies from thousandths of a second for action photography in bright conditions, to many hours for dark sky astrophotography. Unfortunately, taking long-exposure shots of the sky is complicated, because the earth rotates. Hence, exposure time is minimized. Meanwhile, sensitivity can be adjusted, but sensor noise increases with sensitivity. Therefore, a large aperture is advantageous for astronomical observation.
Amateur telescopes with diameters of 4” to 12” are common, while research telescopes can be on the order of meters.
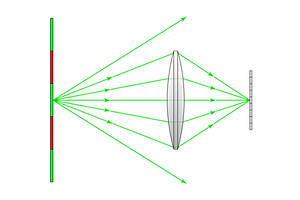
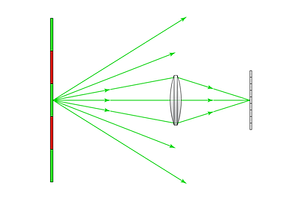
A larger aperture (left) collects more light from each point than a smaller aperture (right)
This principle applies in the animal kingdom as well: nocturnal animals tend to have relatively large eyes.


Left: Owl
By GalliasM - Own work, Public Domain, source
Right: Brown Greater Galago (Bushbaby)
By Jacobmacmillan - Own work, CC BY-SA 4.0, source
Next, we will discuss focal length. Focal length determines the field of view of the lens. Colloquially, people sometimes (incorrectly) refer to this as the “zoom” of a lens - a telescope with a long focal length will appear further “zoomed in” than a telescope with a short focal length.
Consider the two imaging systems shown below: the first system uses a 500 mm focal length lens, while the second system uses a 1000 mm lens. Both systems use a 36 mm wide sensor - a common size in DSLR cameras (known as full-frame format.)
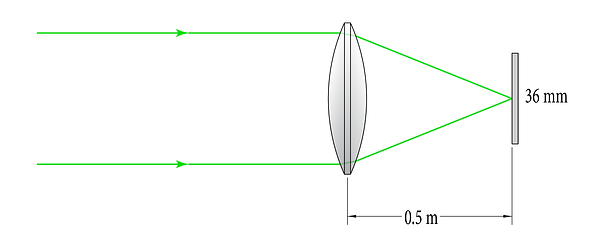
0.5 m focal-length system focusing on-axis rays on a 36mm sensor (not to scale)

1 m focal-length system focusing on-axis rays on a 36mm sensor (not to scale)
Next, observe how each system handles off-axis light. The term “field angle” refers to the deviation of a given beam of light from the normal axis. A 1° field angle is shown in red:
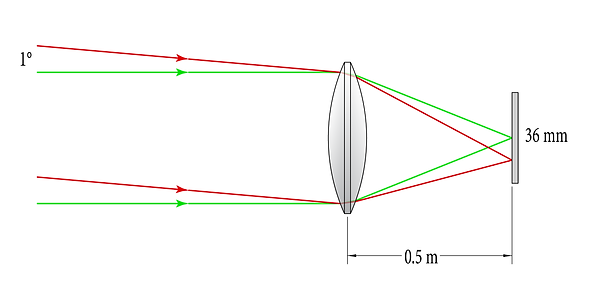
0.5 m focal-length system focusing on-axis rays (green) and 1°rays (red) on a 36mm sensor (not to scale)
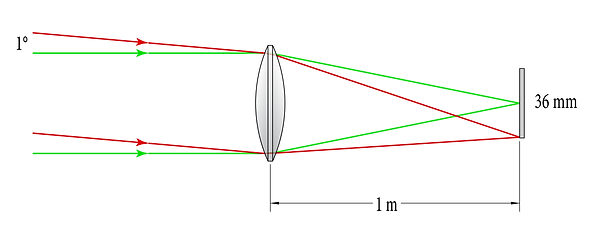
1 m focal-length system focusing on-axis rays (green) and 1°rays (red) on a 36mm sensor (not to scale)
Notice where the various beam angles hit the sensors, respectively. For the 1 m system, a beam 1° off center reaches the edge of the sensor. For a 500 mm system, the same beam only reaches halfway to the edge of the sensor. It would require a 2° field angle to reach the edge of the sensor:
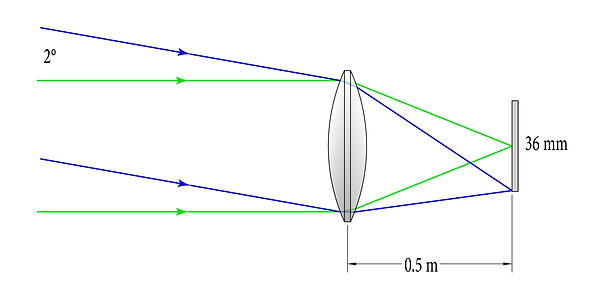
0.5 m focal-length system focusing on-axis rays (green) and 2°rays (blue) on a 36mm sensor (not to scale)

This shows us that the sensor of the 1 m system is “filled” by looking at a 2° cone of sky, whereas the sensor of the 500 mm system is filled by looking at a 4° cone of sky. (To calculate the field of view, double the field angle - because it is symmetric on both sides of the optical axis.) Another way to describe this effect: the 1 m system is “zoomed in”, and can therefore image a given area of the sky in greater detail, whereas the 500 mm system is zoomed out and can image a larger section of sky in a given frame.
For the above diagrams, it is assumed that a 1° field entering the lens will also exit the lens at 1° relative to the axial field. This simplification uses paraxial approximation - but the reader should keep in mind that this approximation is a source of aberration (discussed later.)
The reader might wonder why we don't specify lenses by their fields of view; Wouldn’t this be a convenient method of determining whether our target would fit in the frame? If sensor size did not vary, then yes. But sensor size is not consistent: linked is a diagram of common sensor sizes. When we change the size of the sensor for a system with a set focal length, the field of view of the system changes. For example, when we switch the 36mm sensor in the 500 mm FL system with a smaller 24 mm sensor, the field of view changes from 4° to 2.6°:
0.5 m focal-length system focusing on-axis rays (green) and 1.3°rays (orange) on a 24 mm sensor (not to scale)
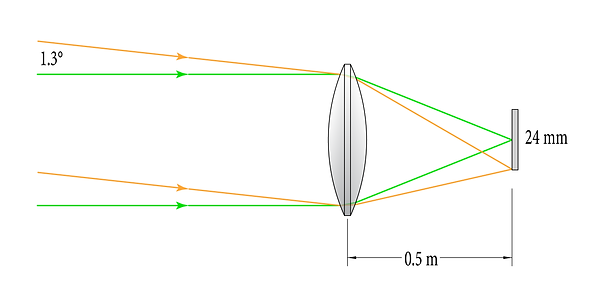
At this point, it is worth noting that since sensor size is tied to angular field of view, rectangular sensor formats will have differing fields of view for each axis.
Conventionally, telescopes are specified by Focal length and F-stop (as are camera lenses.) F-stop is calculated as aperture divided by focal length. For example, a 100 mm aperture lens with a 1000 mm focal length = F/10. Camera lenses are specified the same way.
By Rhcastilhos and Jmarchn.
Schematic_diagram_of_the_human_eye_with_English_annotations.svg, CC BY-SA 3.0, source
Instead of using a sensor to capture an image, we can instead view the image with our eyes. This practice is called visual astronomy (as opposed to astrophotography.) From an optomechanical perspective, digital sensors are simple: they are flat rectangles comprised of evenly-spaced pixels. On the other hand, the human eye is an incredibly complex biological mechanism. It is full of fluid, blood vessels, muscles, features the Zonule of Zinn (which is not a legendary broadsword) - and other parts that I won’t pretend to understand. Instead, we will simplify eyeball to a system with which we are familiar: a sensor behind a lens.
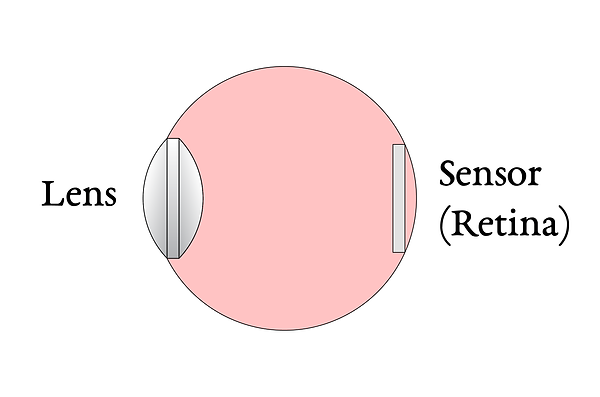
The human eye, simplified
Unlike in the imaging systems previously considered, the geometry of the eye can be adjusted. For example, the aperture size of the eye changes in response to the brightness of the environment. When we enter a dark room, it takes time for our eyes to “adjust”: this is the time required for the pupil to expand, allowing more light to enter the eye. This effectively increases the dynamic range of the eye. (The range of brightness in which an imaging system can operate is termed the dynamic range.)
In addition, by tensing and relaxing muscles, the human eye is able to change the shape of the lens - and therefore the focal length. When a person looks at a close object, the lens functions as depicted in the first image below, whereas when a person stares up at the night sky, the lens functions as depicted in the second image:
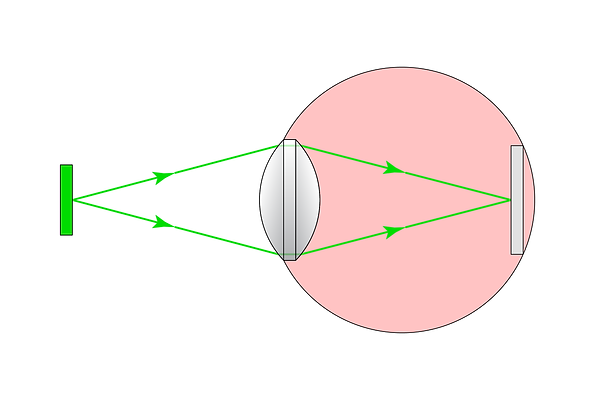
Eye lens shape while focusing on a close object

Eye lens shape while focusing on a distant object
When observing the sky, the best user experience is achieved when allowing the eye to focus on a distant object, as if the adjacent telescope isn’t present. Therefore, telescopes are designed to send parallel beams of light at the eye. This setup provides two additional advantages:
-
As the user moves their eyeball toward / away from the telescope, the eye does not have to refocus (because the light rays are parallel.)
-
In order to focus on distant objects, the muscles of the human eye relax. This allows the user to observe space for hours on end without tiring their eyes! (Conversely, optometrists recommend focusing on a distant point for twenty seconds every twenty minutes focusing on a close object. If you have read this far in one go, you should probably give your eyes a break.)
This effect can be achieved by placing a second lens past the focal point of the objective (first) lens such that their focal points coincide, as shown below. The second lens is often packaged in a replaceable eyepiece.
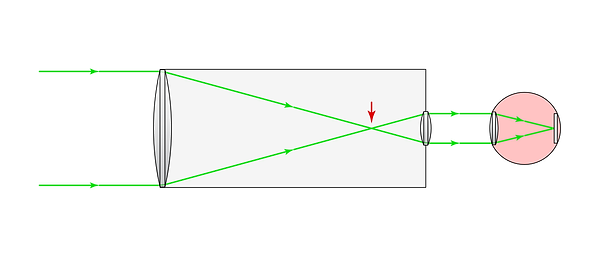
Light rays enter the objective lens of the telescope, exit the eyepiece lens, and are focused on the retina. The common focal points of the objective lens and eyepiece lens are marked by the red arrow.

The objective lens condenses all incident rays such that they enter the eye. Since the area of the objective lens is larger than the area of the pupil, objects appear brighter through a telescope than they would to the naked eye. In addition, the configuration above provides magnification. While the general concept of magnification may not be foreign to the reader, it is worth defining it in this context:
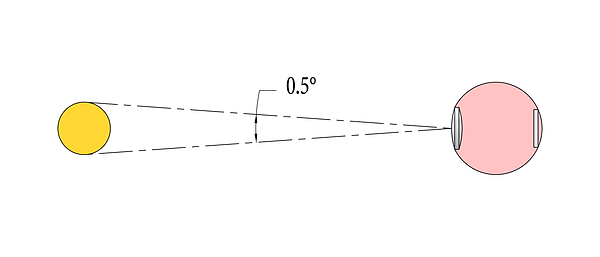
Normally, when we talk about the size of an object, we use units of length. However, when our eyes are concerned, it makes more sense to measure an object by the angular range of our field of view which it occupies. For example, the diameter of the moon is 2,160 miles - but a person couldn’t know that simply by looking at it. Instead, one could definitively say that the moon occupies about 0.5° of their field of view.
.png)
The moon, as observed by the naked eye. The moon occupies about 0.5° of the sky. (Not drawn to scale.)
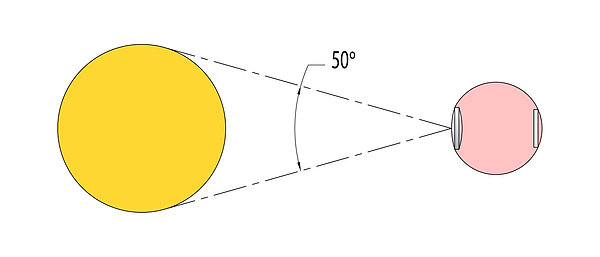
Looking through a system with magnification of 100x: the moon’s 0.5° appears as 50° - enough for the human eye to resolve much more detail.
.png)
The moon, as observed through a system with 100x magnification (Not drawn to scale.)
The angular size of an object depends on the location on the retina at which the rays converge. Previously, we saw where on-axis rays converge on the retina. Now, observe where a field angle of 3° converges:
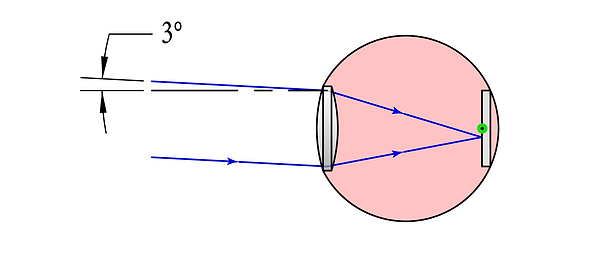
A field angle of 3° is focused on the retina by the naked eye. On-axis rays are focused at the green point.
The apparent size of the object is determined by the area of the retina that it covers. In this case, it is the distance from the 0° field to the 3° field. Now, observe where a field angle of 3° is focused when observed through a telescope:
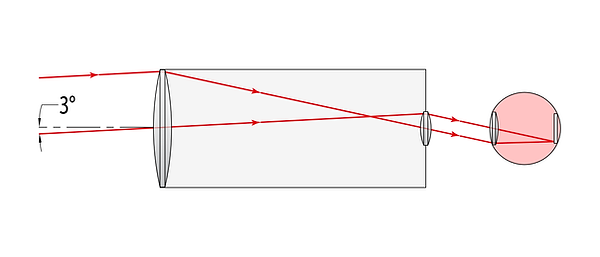
A field angle of 3°, observed through a telescope
The same field angle now falls at the edge of the retina. The object occupies the entire field of view. Stated otherwise, it looks much larger. The reader may notice that the image has been flipped: to the naked eye, a field angle of +3° falls on the bottom half of the retina. Through a telescope, a field angle of -3° falls on the same half. An image flip is common to imaging systems; When an electronic sensor is used, the image can be flipped in software. During visual astronomy, the flip can be confusing for reckoning - but ultimately it doesn’t affect the beauty of an object. After all, our orientation in the universe is arbitrary!
In the diagram of on-axis rays entering the telescope, it is apparent that focal length of the eyepiece lens is very small compared to that of the objective. The ratio of focal lengths is what gives the optical system its magnification. This effect is described with the simple equation M = Fo/Fe, where M is magnification, Fo is the focal length of the objective lens, and Fe is the focal length of the eyepiece. For example, a telescope with 1 m objective lens and a 10 mm eyepiece will magnify the sky 100x to the observer.
At this point, the reader might wonder what area of the sky we can actually observe at 100x magnification. The human eye has roughly 120° of vision span. Of this, only 6° of span is capable of resolving text. (Most of our vision span is peripheral vision.) Using the above logic, we should be able to observe roughly 1.2° of the sky at magnification 100x. However, most commercially available eyepieces have a limited field of view of less than 90°. Using such an eyepiece, the field of view would be limited to about 0.9° of sky - still enough to comfortably fit the moon in frame. Generally, the eyepiece can be swapped for one of differing focal length; In this way, the size of the area under observation can be easily adjusted.
There is another effect of magnifying an area of sky that must be addressed. While swapping eyepieces changes the magnification factor, it does not change the aperture of the system. The same amount of light from a given area of the sky enters the telescope. When configured with a high magnification, the system effectively spreads this light over a larger area of the retina - and thus that area of sky will look dimmer than it would at a low magnification. This effect is demonstrated in the images below.

The moon as observed by the naked eye

The moon as observed through a system with magnification 4x, without increasing aperture size
By Tomruen - Own work, CC BY-SA 4.0, source
Astronomers quantify the apparent magnitude of celestial objects. The brightness of a celestial object through a telescope can be calculated as:
(Apparent magnitude) * (Area of the telescope aperture) / (Area of the human pupil - about 23.8 sq. mm in low-light conditions) / magnification.
Mirrors or Lenses
Until now, we have used lenses to focus light. Such a telescope is classified as a refractor. However, light can be focused by another method: a curved mirror can be used instead of a lens. Mirror-based telescopes are called reflectors.
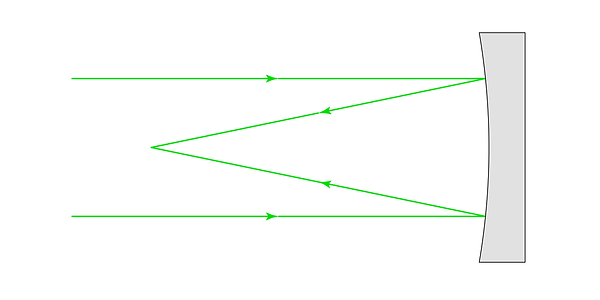.png)
A parabolic mirror will focus parallel incoming rays to a point

The first inherent difference that must be noted when comparing reflectors with refractors is that the layout of a refractor allows the sensor to sit directly inline with the lens. Since the mirror in a reflector telescope reflects the light back in the direction from which it originated, this makes sensor placement more difficult (especially considering that the sensor is generally packaged into a large camera body, or an even larger human head.) In the diagram above, if the camera body were positioned such that the sensor lay at the focal point of the mirror, the body of the camera would block a large portion of the incoming light. This would have a similar effect to reducing the aperture size. Various strategies are employed to solve this problem. The two most common strategies are:
Diagonal mirror: a small secondary mirror is placed in the reflected beam path before the focal point. The mirror is angled at a diagonal (generally 45°), such that it directs the beam out of the main optical path, where a sensor can be placed without blocking the aperture. While the diagonal mirror itself blocks a portion of the aperture, it is sized to block much less light than an entire camera body would.

A diagonal secondary mirror diverts the convergent rays out of the incoming beam path, onto the sensor
Alternatively, the first mirror (the primary) is designed with a hole in the center. A secondary mirror is placed in the reflected beam path such that the rays are reflected once again - through the hole in the primary. The sensor is placed behind the hole in the primary, in line with the axis of the telescope. Once again, part of the incoming beam is blocked by the secondary mirror - but much less than would be blocked by a camera in the same position.
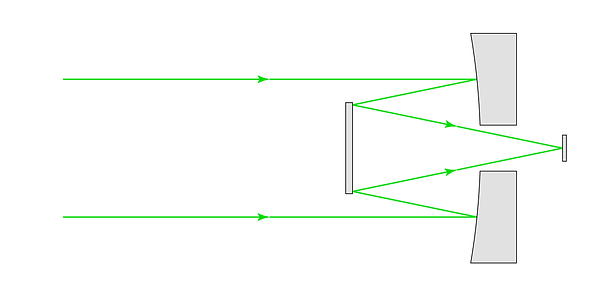.png)
A coaxial secondary mirror diverts the convergent rays out of the incoming beam path, through a hole in the primary, onto the sensor
Virtually all astronomical research is conducted using reflectors. Large-diameter refractor telescopes have some inherent issues that will be discussed below.
Aberrations
Thus far, we have operated under the assumption that there are lens or mirror shapes that can perfectly focus parallel light rays coming from multiple directions. Sadly, this is not the case. For example, while a parabolic mirror perfectly focuses on-axis rays, parallel off-axis rays do not meet at a single point.
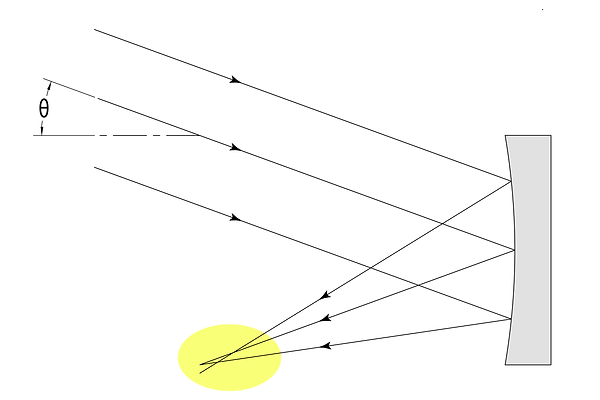
Off-axis rays do not converge when reflected off a parabolic mirror
This shortcoming of optical elements is known as an aberration. While the word would imply that the issue is caused by a malformed mirror, it is important to realize that even a perfectly parabolic mirror will behave in this manner. Unfortunately, all powered optical systems suffer from aberrations. It is impossible to perfectly focus rays of parallel light entering from multiple directions. The magnitude and type of aberration varies system-to-system. For example, the aberration intrinsic to parabolic mirrors described above is known as coma.
Additional aberrations can be introduced due to deviations from the ideal geometry (for example, if the mirror surface above wasn’t formed as a perfect parabola.) These aberrations are described in detail below, in the section titled Wavefront Error.
Ironically, in precision optics, we strive for “good enough.” A sensor cannot differentiate between rays hitting different points on a single pixel. Therefore, as long as all rays in an aberrated beam fall within a single pixel and do not “bleed over” into the next pixel, the aberration will remain undetectable.
Due to an aberration, off-axis rays do not converge at the sensor. However, if the rays only strike a single pixel, the aberration is undetectable.
The size of the area of the sensor onto which the light rays fall is commonly referred to as the “spot size”, and we will use this terminology moving forward. In the image above, axial rays have a spot size of zero (they converge perfectly), whereas the off-axis rays have a spot size almost as large as a pixel.
Pixel size affects a system’s vulnerability to aberrations. For example, if the pixel size were halved in the system above, the field angle shown in red would strike multiple pixels, and therefore the aberration would be detectable:
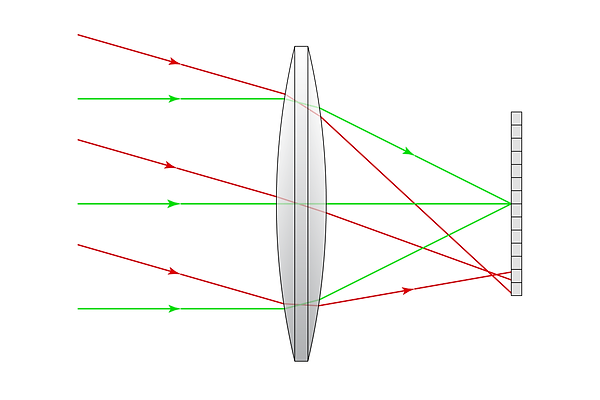
By doubling the resolution of the sensor (halving pixel size), a previously undetectable aberration becomes significant
A noteworthy aberration is field curvature. Let’s imagine a system free of the previously described types of aberrations; In this system, each field angle is focused to a unique point. One might think that we’re scot-free - except that we never specified where these focused points lie. If the focus points lie on a single plane, then we need merely place our sensor on that plane, and voila - a perfectly focused image. However, for many systems, the focus points (or closest-to-focus points, for systems with other aberrations) do not lie on a plane; Rather, they lie on a curve. Attempting to fit a planar sensor to this curve will result in defocus in certain areas of the image.
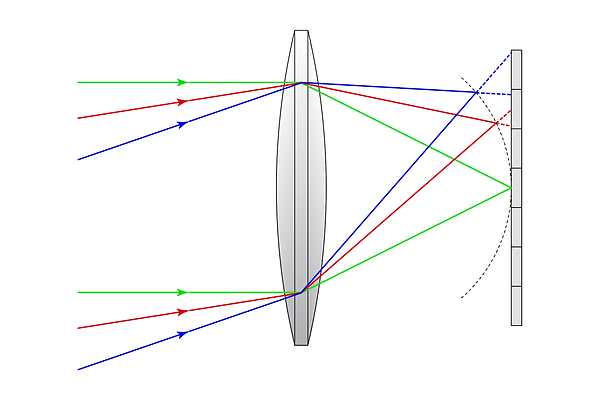
All three sets of rays converge. However, the points of convergence lie on a curve, rather than on the flat sensor; Only the on-axis rays converge to a point on the sensor. The field angle drawn in red still falls on a single pixel by the time the rays reach the sensor, so the aberration is undetectable. However, the field angle drawn in blue diverges enough to cover multiple pixels, therefore this affects the final image.
Special curved sensors have been constructed to match field curvature, but this is not a solution that is available to consumers. Another solution designed to mitigate the effect of field curvature is to use a smaller sensor. This effectively reduces the field of view. Since field curvature worsens as field angle increases, the effects are reduced. (This is equivalent to cropping out the problematic fields.) To compensate for the reduction in field of view, mosaics of multiple adjacent images are constructed, to cover areas that do not fit in a single frame. This has the added benefit of producing a much higher-resolution image than could be captured with a single shot.
Refractor telescopes may suffer from an additional issue known as chromatic aberration. Simply put: lenses do not bend differing wavelengths of light equally. This is commonly known as the “prism effect.” Chromatic aberration can lead to interesting effects, such as fringing. Methods exist to compensate for chromatic aberration in refractors - but these methods introduce additional trade-offs that we will not cover here. Luckily, mirrors do not exhibit a prism effect, and therefore reflector telescopes do not suffer from chromatic aberration.

Due to chromatic aberration, blue light is refracted at the greatest angle, followed by green, then red. In this example: the blue rays converge to a point, the green rays converge to a single pixel (and therefore the aberration is undetectable), but the red rays strike multiple pixels. Displayed, this would appear as a blue-green-tinted pixel, surrounded by a halo of red pixels.
Vignetting
Most optical systems suffer from another imperfection: the portion of light that reaches the sensor varies depending on the field angle. For example, consider the aforementioned refractor with eyepiece:
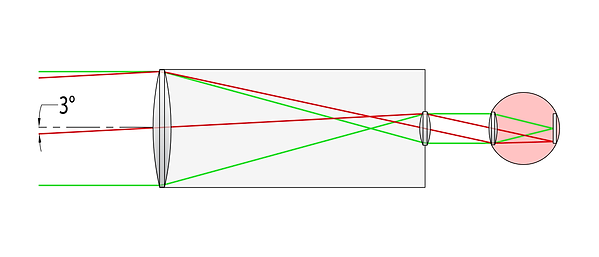
A refractor telescope with objective and eyepiece lenses
The axial rays are drawn entering at both extremes of the objective lens. However, the 3° field is drawn such that it only spans the top half of the lens. Let’s examine what happens to rays that enter the bottom half of the objective:
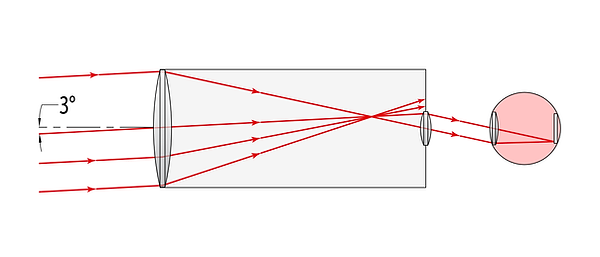
The newly drawn rays miss the eyepiece lens completely, and hit the inner wall of the telescope. Thus, in this system, all axial rays incident on the objective reach the sensor, but only half of the 3° field rays reach. If an object of uniform brightness is photographed with this system, the center of the image will appear full brightness, and the image will appear darker near the edges. This effect is known as vignetting.

The edges of this image are darker than the center, due to vignetting of the camera lens
By TheDefiniteArticle - Own work, CC BY-SA 4.0, source
Both refractor and reflector telescopes can suffer from vignetting:
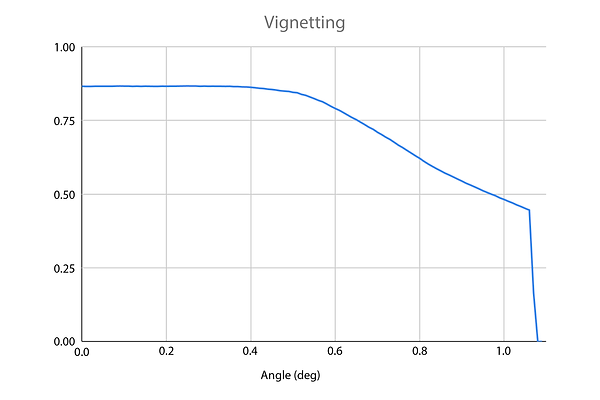
A plot of the portion of light that reaches the sensor vs. field angle for a Newtonian reflector
The severity of the vignetting depends on the geometry of the design. The effect can be adjusted, but this often comes with a trade-off. For example, the effect of changing the diameter of the secondary mirror is plotted below:

Vignetting for various sizes of secondary mirror in a Newtonian telescope
The green line shows the vignette effect from using a 104 mm secondary mirror. The line remains flat from 0° through 0.5° field angles, at which point it begins to vignette. Compare this to the blue line, which marks vignetting from a smaller 74 mm secondary: while vignetting begins to occur much earlier (around 0.2°), the amount of light collected at each field angle is greater. This is due to the portion of the aperture blocked by the secondary mirror. At ~1.1°, all of the curves drop to zero, as the field hits the side of the eyepiece, rather than passing through the lens. (Ultimately, the mirror represented by the red line was selected - it provided a good tradeoff between vignetting effects and total light collection.)
While vignetting is intrinsic to the optical system, it is sometimes increased in post-production for artistic effects. This can be done with software such as Photoshop - in fact, many modern smartphones have an adjustable vignetting “filter” built in to the native software.
With respect to astrophotography, vignetting is a double-edged sword. Since aberrations tend to worsen near the edge of an image, vignetting may make these effects more difficult to detect. However, for scientific observation, a uniform measurement of intensity across the image is generally preferred. Just as vignetting can be increased in post-production, it can also be negated. For example, Photoshop features a library of lens profiles for many commercially-available camera lenses, and can therefore compensate for vignetting, as well as several types of aberration. Custom lens profiles can also be created.
Telescope Architectures
We now have the tools to discuss specific telescope architectures. There are many variations of refractors and reflectors (as well as a third category - catadioptric telescopes, that use both mirrors and lenses), but we will focus on three specific architectures - because they are the types that I have modeled.
The Newtonian telescope (named after its inventor: Sir Isaac Newton) uses a concave parabolic primary mirror to focus light. A diagonal secondary mirror redirects the reflected light out of the main beam path, such that the sensor (or eyepiece) does not block the aperture. Since Newtonians use a flat secondary mirror, the placement of the secondary is not as critical as it is for systems that use multiple powered (curved) elements; This simplifies the design and calibration process. However, this simplicity comes at a cost: due to the mechanical layout, Newtonians tend to be nearly as long as the focal length of the system - longer than other telescope architectures. In addition, the use of a single powered mirror has optical downsides as well: while light parallel to the optical axis can attain perfect focus, off-axis light suffers from an aberration called coma, described above. Several companies make coma correctors: lens-based modules that mitigate this effect.

Diagram of a Newtonian Reflector
The Cassegrain reflector uses a concave parabolic primary mirror with a hole in the center, and an on-axis convex hyperbolic secondary mirror to bounce light back through the hole in the primary, where the sensor (or eyepiece) is positioned. Since both mirrors are powered (curved), alignment of the mirrors is critical. However, this architecture allows for a distinct mechanical advantage: because the light path zig-zags through the entire length of the system, the telescope can be much shorter than a Newtonian of the same focal length - about half as long. Cassegrains suffer from both coma and field curvature issues - both of which cause additional blurriness toward the edge of the image.
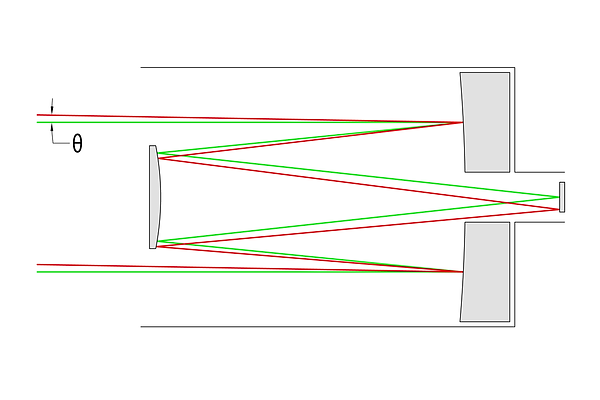
Diagram of a Cassegrain Reflector
The Ritchey-Chrétien telescope is a Cassegrain variant. Instead of using parabolic primary and hyperbolic secondary mirrors, it uses two hyperbolic mirrors. This tweak eliminates coma, but the design still suffers from field curvature. Several companies make field flatteners: lens-based systems that mitigate this effect.
Wavefront Error
Physics students are well-versed with the phrase: “ignoring air resistance…” Air resistance is a complicated topic! For this reason, new physics students are instructed to ignore it altogether as they study the basics of motion, forces, and momentum. Later, they are told that the force of air resistance is equal to the cross-sectional area of the object multiplied by air velocity squared. Next, they take their first fluid dynamics class - the concepts of turbulent and laminar flow are introduced - and they realize that the problem is more complicated yet. Thus far, we have operated “ignoring air resistance” - in an imaginary world free of complexities. Let’s take the next step toward reality!
The issue that we must address is that in an optical system, the surfaces of the elements will never perfectly match the mathematically defined profiles that we discussed earlier.
While exploring this topic, we will use industry-specific terminology to describe the deformation of an optical surface:
The optics industry measures deviation from the ideal profile in units of waves of light, rather than a standard unit of length (such as nanometers.) The deviation is therefore termed wavefront error. The rationale behind this unconventional metric is that the performance of an optical system depends on the wavelength passing through it. (For this reason, reflectors for radio dishes are sometimes constructed out of mesh panels: at those long wavelengths, mesh “looks smooth”. However, a mesh panel would be completely insufficient as a mirror for visible light, which has much shorter wavelengths!)

For example, a deviation of 460 nm would be measured as 1 wave of error for a system designed to handle blue light, but would only constitute 0.8 waves of error in a system meant to handle yellow light. For a system designed to operate across a range of wavelengths (such as a telescope), the wavelength is generally selected in the middle of the range - I.E. 550nm (green light.)
When quantifying the form accuracy of an element (lens or mirror), the root-mean-square of the deviation across the surface is given, in waves.
Then, in order to quantify the optical performance across an entire system, the wavefront error of the individual elements is combined. The strategy for combining error varies based on the type of error - for example, in certain scenarios, wavefront error on consecutive elements will actually cancel out! But, a common method is to calculate the RSS error of the elements in the system.
We will not discuss the diffraction limit of optical systems in detail here, but for interested readers: a system with Strehl Ratio of 0.8 (which corresponds to a wavefront error of ~0.075 waves) is generally considered diffraction-limited.
It should be noted that the specific effect that wavefront error has on a system depends on the shape of the error. There are literally infinite ways in which a surface could deviate from the target profile, and each unique surface will steer light differently when integrated in a system.
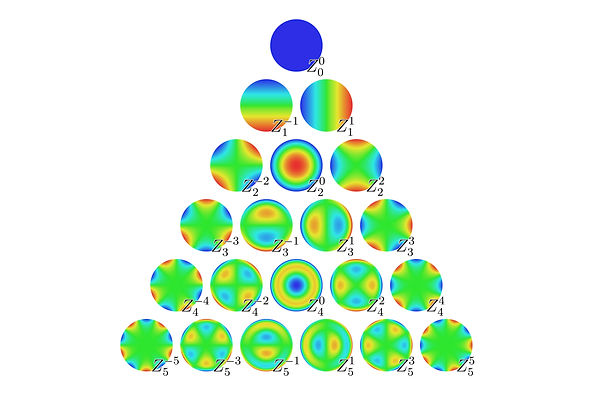
In standard practice, the shape of error on an optical element is described as a weighted sum of orthogonal Zernike Polynomials. The first 21 polynomials are shown above, but the series is infinite.
By Zom-B at en.wikipedia, CC BY 3.0, source
To build an intuitive understanding of how wavefront error affects optical performance, I ran some simulations: I took the model of one of my telescope mirrors, and deformed it in simulation. The specific shape of the deformation was chosen based on an estimate of real-world conditions (more on that topic below.) I then modeled the effect on the telescope’s ability to focus beams of light, and graphed the results:
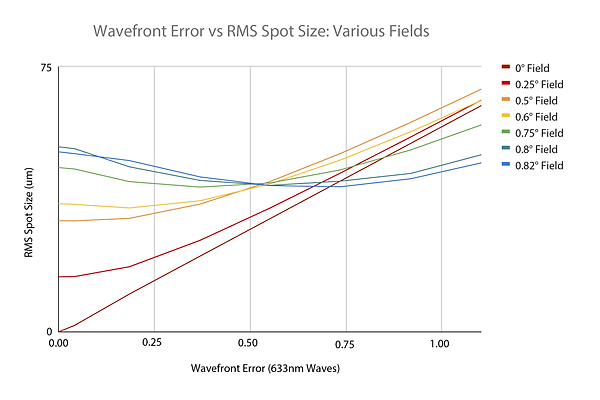
Primary mirror wavefront error vs spot size for a Newtonian telescope
The graph displays the focused spot size with respect to wavefront error, across multiple field angles. Notice that certain field angles never reach a spot size of 0, even when the system is without wavefront error; This is due to inherent aberrations such as coma and field flatness, which were discussed earlier. It is also noteworthy that for certain field angles, the deformations can actually decrease the spot size. At those angles, the deformations are counteracting the inherent aberrations, and the telescope actually focuses better than it otherwise would!
Now, let’s discuss the factors that contribute to wavefront error in our system. These factors fall into two categories:
Wavefront error caused by deformation of the optical elements:
-
In its resting state, an optical element will have aberrations due to manufacturing tolerance. A high quality consumer grade telescope mirror will match the ideal profile to within 1/16 waves RMS, (which equates to ~34 nm RMS), prior to being installed in a system. For reference, this deviation is extremely small: it means that the RMS deviation is within 1/2500 the width of a human hair, or 127 times the diameter of an aluminum atom! As one might imagine, precisely machining a material at the atomic scale is quite difficult, and is done with single point diamond cutting or grinding machines.
-
Once installed in the system, the element will deform under gravity: this is commonly referred to as “sag”. Earlier it was mentioned that large refractor telescopes are rare: since lenses can only be supported by their outer profile, lenses suffer particularly from gravity-induced sag. (Mirrors can be supported by the profile as well as the entire back surface.) This becomes especially problematic for large-diameter lenses: the support area scales with diameter squared, but the volume (and therefore mass) scales with diameter cubed. This same principle explains why ants can carry 50x their body weight, and why large animals tend to be sphere-shaped.


Large animals tend to be sphere-shaped, compared to small animals
Hippopotamus: By Diego Delso, CC BY-SA 4.0, source
Spider: By Olei - Self-published work by Olei, CC BY-SA 3.0, source
-
An optical element may deform as a result of how it is being constrained by the adjacent supporting parts. For example, if retention springs are used, the springs impart a force on the element. Or, if adhesive is used, shrinkage during the cure phase may impart stresses on the element.
-
As ambient temperature changes, the overall dimensions of the element change proportionally. For a powered element, a change in focal length will result. In addition, if the temperature change is rapid enough, a temperature gradient may result within the element itself, which can lead to internal stresses and non-proportional deformations. (Think of pulling a glass bottle out of a flame and submerging it in cold water.) Internal stresses may have a secondary effect on lenses, apart from simply deforming the profile: birefringence.
-
Furthermore, coefficient of thermal expansion (CTE) mismatch between the element and the adjacent parts must be considered. For example, if a glass mirror with low CTE is adhered to an aluminum plate with high CTE, then the aluminum plate will contract more rapidly than the glass as the night cools. This will impart a stress on the mirror, deforming it.
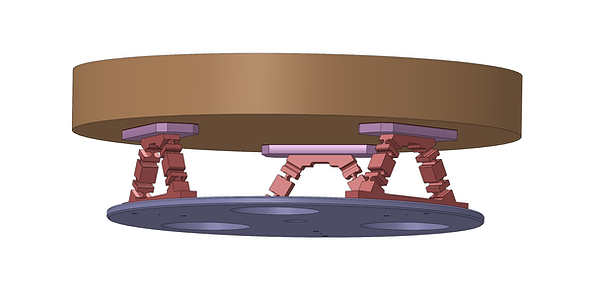.png)
A rendering of a flexure-based mirror cell supporting a 250 mm diameter glass primary mirror for a Newtonian telescope. The flexures allow for disproportionate thermal expansion of the mirror (orange) and supporting plate (purple) without imparting stress on the parts.
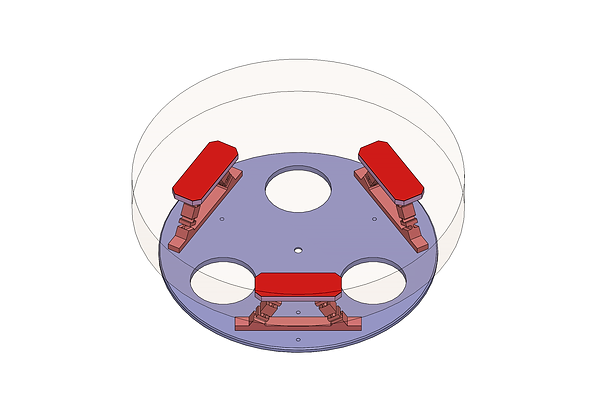
The size and location of the support pads are carefully chosen to minimize mirror sag, as are the mechanical and thermal properties of the adhesive (shown in red.)
Misalignment of the optical elements due to the mechanical structure of the system:
-
Just as gravity can deform individual optical elements, it can deform the overall structure of a telescope - causing misalignment between the individual optical elements (and the sensor.) This is especially relevant for telescopes that can be steered to look at different areas of the sky: as the telescope is reoriented relative to gravity, the structure will flex under its own weight.
-
Similarly, thermal issues must be considered for the overall structure. As the ambient temperature changes, the mechanical components comprising the structure will expand and contract. This can often cause focus issues: if a sensor is positioned at the focal point of the system early in the night, it may creep forward (out of focus) as the system cools overnight, leading to defocused images.
-
Calibration: the “macro structure” of a telescope is often designed with loose tolerances, and the elements are nudged into their final positions with fine calibration mechanisms. The calibration stage generally requires external components such as LASERs, cameras, artificial stars, and additional mirrors or lenses. The positional accuracy of the telescope’s optical elements is governed by the calibration process; A poor calibration can be a source of wavefront error.
-
Vibration: wind can excite modes of vibration in the structure. This is problematic for photography, where vibrating optical elements can cause the beam to sweep back and forth across the sensor array, leading to a blurred image. While this is not strictly a source of wavefront error (that term is generally reserved for static systems) - vibration in the telescope can manifest similar results, and is therefore noted here.
Peripheral Components
Up until now, we have used the word “telescope” to refer to the components in the light path of the system. However, additional components are required in order to create a functioning imaging system.
It should be noted that the scope of the word “telescope” is somewhat ambiguous. Sometimes the word is used to refer solely to the static portion of the optical assembly; For a newtonian telescope, this would include the primary and secondary mirrors, and mechanical structure that houses the mirrors. (For specificity, this portion can be referred to as the Optical Tube Assembly, or OTA.) Other times the word is used to refer to the entire imaging system, including the sensor, eyepiece, mount, and other peripheral equipment that will be covered later. This ambiguity probably stems from the fact that not all systems are designed with interchangeable components, and therefore some imaging systems cannot be disassembled into separate parts.
The Mount
The fact that the earth is rotating in space complicates astronomy. The speed of rotation is roughly once in 24 hours; This is equivalent to 15° per hour, or 1° every four minutes. When we previously discussed magnification, we described a system with a 0.9° field of view in order to observe the moon. If we were to aim a statically-mounted telescope at the moon, then within four minutes, the moon would be fully out of the frame (because the earth will have rotated 1° in that time!)
Therefore, adjustable mounts are used to reorient the telescope. The simplest type of mount is the Altazimuth mount: adjustable vertical and horizontal axes allow the telescope to be pointed anywhere in the sky.

A telescope mounted to a manually-adjustable Altazimuth mount
Rotation of the earth presents an even greater challenge when the system is used for astrophotography. Often, long-exposure frames must be taken in order to collect enough light to image faint objects. If the telescope isn’t synchronized with the rotation of the earth, the result would look like this:

Static long-exposure photograph of the night sky
By Akiyoshi's Room - Akiyoshi's Room, Public Domain, source
Therefore, motorized mounts can be used to counter the earth’s rotation, and point the telescope at a fixed point in the sky.
Equatorial mounts similarly use two orthogonal rotation axes. However, unlike for an altazimuth mount, one of the axes is aligned to be parallel to the rotation axis of the earth. Both axes are initially adjusted in order to aim at a celestial body. Once the telescope is aligned, the parallel axis can be rotated at the same speed as the earth, but in the opposite direction. This reduces error relative to a tracking altazimuth system, which requires that both axes be continuously adjusted in order to properly track the sky.

A telescope mounted to an equatorial mount. The rotation axis marked in green is aligned parallel to the earth’s rotation axis.
Modern systems may include Go-To functionality - a computer system that stores the location of thousands of celestial objects. Once the mount is homed at the start of the night, it can be commanded to automatically find (and track) any object in the library. This gives modern-day astronomers a huge advantage over past generations!
Guide Scope
A second small telescope (equipped with its own sensor) is often attached directly to the main telescope. The output of this sensor is fed back to the tracking mount and provides closed-loop feedback to the system, improving the accuracy. If the tracking mount drifts out of position, a computer reading the guide scope notifies the system, and the mount can rectify its heading. Interested readers should research off-axis guiders as a lightweight and accurate alternative - but I will not cover these devices here.
Finder scope
It can be difficult to identify the area of sky viewed through the main telescope; Magnification and change in apparent magnitude can make the sky appear very different than it does to the naked eye. Therefore, an additional small telescope is used as a “stepping stone”. This telescope is attached to the main telescope, and is aligned to be parallel to the OTA’s axis. This scope is equipped with an eyepiece, and covers a relatively wide field of view (e.g. 5 degrees, with a magnification of 10x.)
A Cassegrain telescope mounted to an equatorial Go-To mount. A guide scope (white) is attached to the main telescope, as well as a small finder scope (black.)
Kapege.de / CC BY-SA, source
The Camera
The camera houses the delicate sensor in a body. Attention must be given to ensure that the sensor is a good fit for the rest of the system. For example, earlier it was shown how sensor size affects field of view. One might think that a higher-resolution sensor automatically leads to higher-resolution images, but this is not the case; Assuming a fixed sensor size, doubling the number of pixels means halving the area of each pixel. If the optics are unable to resolve light rays to a small enough spot size, then the spots of light effectively “bleed over” into adjacent pixels, thus the doubling of resolution is irrelevant.
Dedicated astrophotography cameras are commercially available. These cameras differ from standard DSLR cameras in several ways:
-
AP cameras generally do not have viewfinders.
-
Sometimes, smaller sensors are used in order to mitigate field-curvature and vignetting. To maintain resolution, these AP cameras generally feature smaller pixels than are found on conventional digital cameras. As mentioned previously, small pixels are only beneficial if the resolving power of the optics is adequate.
-
High-end AP cameras will include a thermoelectrically-cooled sensor. Image noise increases with temperature, so a cold sensor can lead to noise-free images.
-
AP cameras are often monochrome. Technically, all digital camera sensors are monochrome, but off-the-shelf digital cameras feature a Bayer filter over the sensor, as well as UV and IR filters. The ratios of red, green, and blue tiles in the Bayer array are optimized to emulate photopic response of the human eye to a world illuminated by our sun. With respect to the spectral content of the rest of the universe, this is an arbitrary “optimization”, and it can work against the photographer while imaging certain celestial bodies. For example, if a very blue body is being photographed, the existence of a Bayer filter becomes problematic. During the duration that would properly expose the blue pixels, the red and green pixels would be severely starved for photons. So, additional longer-exposure frames might be used to try to collect sufficient red and green data - but the blue pixels will oversaturate during the same period. Sorting through this mess in post production can be arduous; In addition, since each exposure is essentially being used to collect a single color channel, ⅔ of the data per frame is effectively discarded. This is where filters come in.

Consumer-grade digital cameras feature a Bayer filter over a monochrome sensor
By en: User: Cburnett - Own work, CC BY-SA 3.0, source
Filters and Filter Wheels
By using a monochrome camera and dedicated bandpass filters, a photographer gains control over the exposure time at each spectral band. Thus, the shot can be tailored to match the target’s spectral bandwidth. The separate images can be combined in post production, where each color channel can be manipulated independently. Filters are available in many different colors, as well as infrared and UV.
Multiple filters can be installed into a filter wheel. This mechanism is placed between the telescope and the camera. The wheel can be rotated - moving each filter into the beam path one at a time, without detaching the camera from the telescope. This prevents the photographer from needing to refocus the system each time a filter is swapped. In addition, motorized filter wheels can be used to automate exposures with different filters throughout the night.

A filter wheel is mounted between a monochrome camera (blue) and the telescope
© Marie-Lan Nguyen / Wikimedia Commons, source
Other equipment
Astronomers use a myriad of other equipment during a night of imaging. An electronic autofocuser might be used to move the sensor into focus. A computer running astrophotography software may be used to control the aforementioned hardware. Electric heaters may be used to prevent dew from building up on the optical elements. An electrical supply is required to power the system. High powered LASERs may be used as an alternative to finder scopes. The list goes on, but I will leave additional research to the reader!